Panda3D memo
Panda3D
Showbase
- グラフィックディスプレイを開いたり,Pandas3Dでモデルを読み込んだり(loader),カメラやタスクマネージャー(taskMgr)を管理したりするトップオブジェクト。
- ShowBase()すると,グローバルにbase, render, cameraとかのインスタンスが作られるマニュアル。よって,一度ShowBaseのインスタンスを作れば,Pythonインタプリタからは,これらの自動生成インスタンスにアクセスすることが出来るようになる。Built-in Global Variableと呼ぶようで,その一覧はここ。サンプルを見ても,これらのインスタンスが見えていることを前提にした書き方になっている。これはすごく嫌な仕様だな・・・。プロトタイプでは良いけれど,大きなプロジェクトではこの記述は避けるように,とマニュアルに書かれているが,別の正式な方法があるのかな??
Camera
- ShowBaseのインスタンスを生成すると自動的にcameraインスタンスがPythonのGlobal空間に生成される。
- camera.setPos()しても,なぜか思い通りにカメラが動かなくて困ったが,これはデフォルトのマウスによるカメラ移動をOffにしていないから。TaskMgr経由でカメラを動かすと毎時動いているからか問題にならないみたいだけど,一回だけカメラを動かす,と言うときにはマウスのカメラ操作機能を切る(disableMouse())する必要がある。
- カメラの初期位置を設定した後に,マウスのカメラ操作をOnにすることは出来ないようだ。Onにすると,デフォルトの位置に戻ってしまう。その場合は自分でマウスに依るカメラコントロールを書く必要がある,が,これは別に難しくはない。
- カメラはbase.cameraの自動生成のものだけでなく,panda3d.core.cameraで追加することも出来る。
# ウィンドウを分割して2つのカメラの画像を表示する例 from direct.showbase.ShowBase import ShowBase from direct.showbase.Loader import Loader from panda3d.core import * # Loading Model base = ShowBase( ) model = loader.loadModel( "models/misc/rgbCube" ) model.reparentTo( render ) model.setPos( 0, 5, 0 ) #y: depth # z: upper # Subcamera displayRegion = base.win.makeDisplayRegion(0.2, 1, 0, 1) displayRegion.setClearColor(VBase4(0, 0, 0, 1)) displayRegion.setClearColorActive(True) cam2 = Camera( 'camera2' ) lens = PerspectiveLens( ) lens.setViewVector( 0, 5, 0, 0, 0, 1 ) cam2.setLens( lens ) camNP = NodePath(cam2) camNP.setPos( 0, -16, 0 ) displayRegion.setCamera(camNP) camNP.reparentTo(render) #camNP.reparentTo(base.cam)とすると、メインのカメラの動きに連動する # split dimension dr = base.cam.node().getDisplayRegion(0) dr2 = camNP.node().getDisplayRegion(0) dr.setDimensions(0, 0.5, 0, 0.5) dr2.setDimensions(0.5, 1, 0, 1) base.run( )
Scene Graph
- SceneGraphはレンダリング対象を保持するデータ構造。ルートに"render"オブジェクトがあって,その下に階層的にオブジェクトが保持されている形式。
- モデルを読み込んだら,renderなりの子供に指定する(reparentTo)ことでSceneGraphに登録する。そうすると,レンダリング対象となる。
Task
- 毎フレーム呼び出される手続き。
- task.timeはtimestep (elasped time)
- taskMgrは,タスクがAsyncTask.DS_cont(定数)を返す限り,毎フレーム呼び出される。
Actor
- アニメーションするモデルの管理。
- モデルを読み込む際に,静的なオブジェクトはloadModel()を用いて読み込み,動的なオブジェクトはActorを用いる。
- Actorにはモデルのファイル名と,そのモデルの動かし方,の2つを指定して読み込む。
Interval and Sequence (Meta-interval)
- intervalはある期間に渡ってプロパティを変更するタスク。intervalを有効に開始すると,プロパティをバックグラウンドプロセスで開始できる。
- sequenceはmeta-intervalとも呼ばれるもので,intervalのコンテナ。
マウス
- デフォルトで左ボタンで左右,右ボタンで前後,同時押しで視点ベースで回転,真ん中ボタンで世界座標系の中心で回転,する。
- 不要な場合は下記でカメラのマウス操作をオフに出来る。
ShowBase.disableMouse()
メモ
人工知能・深層学習の課題/トピックス
現在の人工知能や深層学習の課題と言われている点を纏めていく。 適時,課題やトピックスを知ったら追記していく。
リスト
- 説明可能性(BlackBox)
- 公平性
- 汎化性
- 大量の学習データや試行,計算資源が必要
- 一般常識
- ベイズとの融合(不確実性の明示的扱い)
- Adversarial Attacks (Security)
- 適切な活用には高い専門性が必要(AutoMLの流れ)
- メタ学習(学習の自動化はAutoMLの流れ)
- Reasoning(Vision-language融合の流れ)
汎化性
ニューラルネットワークは任意の関数を近似することが出来る高い表現力を持つ。しかし,それ故にデータの近傍に過学習している懸念がある。 汎化については下の論文などが改めて議論している。
参考リンク
強化学習の評価環境や機械学習の評価データのメモ
強化学習
OpenAI Gymで知識が止まっていたが,3D環境として最近はUnity-ML-agentが色々と提供しているようだ。ぜひ使ってみる。
OpenAI Gym
強化学習の評価環境と言えばコレ。Atari環境だけでなく簡単な古典制御のClassicやテキストベースのAlgorithmがある。 ロボット環境として2DロボットのBox2Dがある。3Dロボット環境もMujocoが提供されているが,Mujoco自体がライセンスが必要で使い勝手が悪い。MujocoをOSSのPyBulletに置換するRoboschoolも開発されていたが既にDEPRECATEDになっている。Third-partyのPyBullet-Robotics Environmentは使える。 他にもGymと同じ外部APIを定義したThird-partyの環境も多くが公開されているので覗いてみると良い。
VizDoom
Doomと言う1人称視点の3DゲームをAI研究用に提供している。表現学習の例としても使われる。 昔見たときよりも機能が拡充されていた,Detection/Segmentationに使える視覚形式やPythonのAPIも提供されているようだ。
DeepMind Lab
VizDoomと似た目的で使用できそうな1人称視点の3Dゲーム環境。 ただし,環境構築は手間があるように見える。時間があるときに動かしてみよう。
Gym-miniworld
VizDoomやDeepMindLabと類似の目的の環境。Pure-Pythonで環境構築が容易という点がある。
Obstackle Tower
Unityエンジンの3Dゲーム。VizDoomとは違って1人称視点ではない。
Football
サッカーゲームの環境。マルチエージェントや戦略が必要なタスクとして利用できそうだ。
その他
戦略,マルチタスク系ではFootball以外にもStarCraft環境があるようだ。
機械学習
追記する。
Google Colaboratoryのメモ
使い方(Google Driveの利用を前提)
chainerのチュートリアルの最初にGoogle Colaboratoryの使い方がは参考になる。 そもそも,先にgoogle driveの使い方を学ぶ必要があるみたいだ。
- Google driveにログインしてワーキングフォルダを作成する。
- 作成したフォルダに移動し,左上の新規からGoogle Colaboratoryを選択すると新しいノートブックが開く。そのページ自体がJupyternotebookになっている。
- ドライブをマウントするには下記をセルに入力して実行する。実行すると承認確認のURLが生成されているので移動して認証コードをコピーして貼り付ける。適切に承認が出来れば,Google Driveのホームが/content/gdriveにマウントされている状態になる。
from google.colab import drive drive.mount('/content/gdrive')
- マウントしたドライブに書き出してみる。'My Drive'以下にcolaboratory_testでワーキングディレクトリを作成している場合。
with open('/content/gdrive/My Drive/colaboratory_test/foo.txt', 'w') as f: f.write('Hello Google Drive!')
- colaboratoryでは'!'以下にシェルコマンドを記載してシェルを実行することが出来る。例えば,上で作成したファイルを確認する場合。
!cat /content/gdrive/My\ Drive/colaboratory_test/foo.txt
!python test.py # test.pyという実行ファイルをアップロードしている場合
同様にシェルコマンドでgitも使えるのでGithubに上げたコードの実行も簡単。
cdは!じゃなくて%??
環境など
- 90分アイドル状態 or 最大12時間実行でランタイムは消去される。
- メニューの編集->ノートブックの設定,からGPUの使用をOnに出来る。
- 割当ランタイムの確認
!cat /etc/issue # OS version !df -h # Disk !free -h # Memory !cat /proc/cpuinfo # CPU !nvidia-smi # GPU !nvcc -v # CUDA
- pythonのバージョン確認
!python --version #=>Python3.6.9
- インストール済みライブラリの確認。
!pip list
HTML/CSSのメモ
全般メモ
- xxx 全体を要素と呼び,"html"をタグと呼び,タグで囲まれる部分をタグボディと呼ぶ。タグには,xxxのように,属性を適時与えることが出来る。
- HTMLのコメントは\。CSSのコメントはC言語と同じで/ hogehoge /。
- CSSとHTMLの役割分担はHTMLが部品を列挙して,そのレイアウトや色,大きさをCSSで設定する,というイメージ。
- CSSで要素に装飾を施す場合に,各要素はclassにより名前を独自に付与することが出来る。
- HTMLのレイアウトは基本的に上から順番に構成されていく。横に並べたい時はfloatで横レイアウトをいじる。
- 画像を挿入する場合に,全てをfigure>指定する必要は無い。キャプションを付けたい場合や,本文から参照したい場合にfigureで指定する。画像=img,図=figureという感じなのかな。
用語
HTMLの基本用語
- タグとか属性とかどれがどれか普段書かないので忘れる。
<a href="index.html">Hoge</a>を例に。
| 用語 | 意味 |
|---|---|
| タグ | a |
| 属性 | href |
| コンテンツ | Hoge |
| 要素 | 全体 |
DOM:Document Object Model
- DOMはJavascriptでHTMLの要素を操作する仕組みであり,HTMLやXMLをJSから操作するAPIと考えるとわかりやすい。
- HTMLなどのドキュメントをツリーとして扱う。
- document.getElementById('hogehoge');などがDOM操作の例。
- XpathはDOMの上にある,より高位なラッパー。複雑な条件による要素の抽出が,より容易に書けるようになっている。
- 最近は仮想DOMというのも出てきている。
jQuery(write less do more)
- 当時(2006年)の課題は,ブラウザ間の非互換性,Javascriptの低レベル性があった。
- jQueryはブラウザ間のDOM(API)の差を吸収し,アニメーションや非同期処理(deferred)など,より高位な機能を提供した。
- 最近はサーバ主体からクライアントサイド(ブラウザ)に処理が移行しており,HTML5, CSS3, JS自体の進化もありjQueryで実現していたことがブラウザ側で処理されつつある。それら,クライアントサイドの開発を支援するものが,Angular, React, Vueなど。
- 2018年時点では,jQueryは古くて使うべきではないとされ,Reactなどのフレームワークを使うべし,という風潮があるみたい。Web系はライブラリやツールの栄枯盛衰が速いなー。
SPA (Single Page Application)
- 単一ページで閉じたアプリケーション。ページ遷移による表示コンテンツの一切替えではなく, HTMLの一部を切り替えて表示コンテンツを切り替える。GoogleMapとかがまさにそれ。
Ajax
実行方法
- HTMLのscriptタグに直接記載する。ブラウザの開発コンソールから確認する。 scriptタグはheadタグもしくはbodyタグのどこに書いても良いが,一般的にはbodyタグの最後に書かれる。
- javascriptファイル(script.js)を別途用意しておいて,index.htmlにscript.jsを読み込ませる。
いずれの場合においても,HTMLの上にあるscriptタグから順に実行される。
HTML主要タグ
| タグ | 意味 | 属性・備考 |
|---|---|---|
| h | ヘッダ | |
| p | パラグラフ | |
| a | リンク | href |
| img | 画像 | src |
| li | リスト | |
| ul | アンオーダードリスト | |
| ol | オーダードリスト | |
| div | 意味は無い | spanと違い前後に改行が入り,幅・高さを指定可能。 |
| span | 意味はない | divと違い前後に改行が入らず,大きさは文字で決まる。 |
| br | 改行(break) | 終了タグが不要 |
CSSの書き方
- CSSの書き方は辞書データ(JSON)をそのまま書くような書式。
- "p {font-size: 12px;}"のような形式であり,"p"をセレクタ,font-sizeをプロパティ,14pxを値と呼ぶ。
- セレクタにタグを指定するとタグ全体に,クラスを指定するとクラス全体に適用される。タグとクラスを組合せる(p.hoge=pタグのhogeクラス)ことも可能。また,要素毎に指定するには,idによって指定することも可能。クラスは"ドット"で指定,idは”#”で指定する。
- レイアウトはfloatで横に並べて,それを縦に並べて,という感じ。Tkで言うところの,packでやるようなイメージ。グリッド配置は無いようだ。
- コメントはCの/.../形式。(//は駄目。)
p {font-size: 12px;} /* 全てのpタグの,フォントサイズを12ピクセルに指定。*/ .header-a {font-size: 12px;} /* クラスで指定は.で始める。/ h2.header-b {font-size: 14px;} /* タグとクラスで指定。*/ #hoge {font-size: 10px;} /* idで指定は#で始める*/
CSSプロパティ
| プロパティ | 意味 | 例,備考 |
|---|---|---|
| font-size | フォントサイズ | 12px |
| color | 色 | red |
| background-color | 背景色 | white or #FFFFFF |
| border-[bottom/top/left/right] | 境界線 | solid 5px #FF00FF |
| padding | 余白 | 2px 3px (上下,左右) |
テンプレート
<!DOCTYPE html> // HTML5を指定 <html> <head> // ヘッド部分=ページの設定情報 <meta charset="utf-8"> // 文字コード <title>PageTitle</title> // ページタイトル <link rel="stylesheet" href="stylesheet.css"> // CSSファイルの指定 </head> <body> // ボディ部分=ブラウザに表示される部分 xxx </body> </html>
t-sne(Sklearn)の使い方とプロット(Seaborn)
Web上で見る例がMNISTなどのデータセットで書かれている場合が多いので,もっと単純な場合を例にt-sneの使い方をメモしておく。 また,その描画で手こずったのでそのメモもしておく。描画はMatplotlibを使って各クラスを色分けする方法で手こずった。ただ散布図を描いて,各クラスのラベルで色やマーカの形を変えたかっただけ。Excelなら何も悩まない描画なのに,Matplotlibではやたらと手こずる。colorbar, cmapなど色々調整方法を調べたが,結局,Seabornを使うのが覚えやすい(忘れにくい,思い出しやすい)と自分の中では結論。Seabornは最初はPandasのDataframeに変換するのが面倒だ,とも思ったが,Excelとやっていることは一緒なので良しとする。
t-SNEの使い方 in Sklearn
覚えておくことは,fit_transformに渡すデータの形式。渡すデータは,データ数をN,(一般的に高次元な)次元をDとすると,(N,D)のshapeのndarray。これが,(N, 2 or 3)に変換される。
描画
Seabornはscatterplotで散布図が描ける。データはPandasのデータフレームとして渡して,x,yのカラム名を渡す。特に,クラスで色分けする場合にはhueにラベルを渡す。t-sneの結果であるndarrayをPandas.DataFrameに変換する方法は幾つかあると思うが,カラム名とそのカラムのデータをDictionaryとして渡す形式が一番覚えやすい。ほかは渡し方でIndex方向とColumn方向が意図と逆になるなどが煩わしい。
例
ここでの例は,4つのクラスタに別れるようなデータを作っている。64次元の空間に各クラスタのデータ(d1, d2, d3, d4)がそれぞれ中心位置をずらして正規乱数で生成されている。
import matplotlib.pyplot as plt import numpy as np import pandas as pd import seaborn as sns from sklearn.manifold import TSNE # Psedu dataset, (4 cluster). N = 100 # the number of data for each cluster D = 64 # space-dimension d1 = np.random.randn(N, D) + \ np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, # 16 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) l1 = np.array(['0']*N) d2 = np.random.randn(N, D) + \ np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) l2 = np.array(['1']*N) d3 = np.random.randn(N, D) + \ np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) l3 = np.array(['2']*N) d4 = np.random.randn(N, D) + \ np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]) l4 = np.array(['3']*N) labels = np.concatenate([l1, l2, l3, l4], axis=0) dataset = np.concatenate([d1, d2, d3, d4], axis=0) # Reduce dimension by t-sne latent_vecs = TSNE(n_components=2).fit_transform(dataset) # Plot dataset with Seaborn df = pd.DataFrame(data={'x': latent_vecs[:, 0], 'y': latent_vecs[:, 1], 'label': labels}) sns.scatterplot(data=df, x='x', y='y', hue='label', palette=sns.color_palette('hls', 4)) plt.savefig('tsne.png') plt.show()
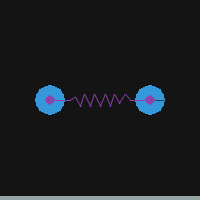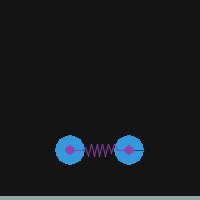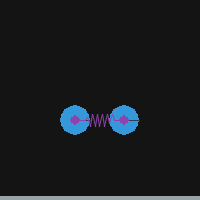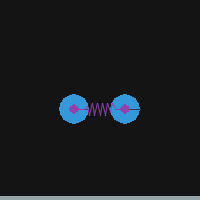
Pymunkでバネ(DampedSpring)を使う
シミュレーションでバネを使う例。
import sys import pymunk import pymunk.pygame_util import pygame as pg from pygame.locals import QUIT, KEYDOWN, K_ESCAPE SCR_W, SCR_H = 200, 200 TICK = 100. def setup_space(): space = pymunk.Space() space.gravity = 0, -100 space.damping = 0.99 return space def setup_pygame(): # Initialize pygame screen for pymunk debug. pg.init() scr = pg.display.set_mode((SCR_W, SCR_H)) clk = pg.time.Clock() draw_options = pymunk.pygame_util.DrawOptions(scr) return scr, clk, draw_options def add_ground(space): b0 = space.static_body ground = pymunk.Segment(b0, (0, 0), (SCR_W, 0), 4) ground.elasticity = 1.0 space.add(ground) return def add_balls_and_spring(space): R = 15 b1 = pymunk.Body(mass=1, moment=10) b1.position = SCR_W/4, SCR_H/2 s1 = pymunk.Circle(b1, radius=R) s1.elasticity = 1.0 b2 = pymunk.Body(mass=1, moment=10) b2.position = 3*SCR_W/4, SCR_H/2 s2 = pymunk.Circle(b2, radius=R) s2.elasticity = 1.0 spring = pymunk.DampedSpring(b1, b2, (0, 0), (0, 0), rest_length=50, stiffness=100, damping=1.0) space.add(b1, s1, b2, s2, spring) return def run(): # Initialize Pygame and Pymunk scr, clk, draw_options = setup_pygame() # Pygame setup space = setup_space() # Pymunk setup # Add objects add_ground(space) add_balls_and_spring(space) # Run simulation t = 0 while True: for e in pg.event.get(): if e.type == QUIT: sys.exit(0) elif e.type == KEYDOWN and e.key == K_ESCAPE: sys.exit(0) scr.fill((20, 20, 20)) space.debug_draw(draw_options) space.step(1/TICK) pg.display.flip() clk.tick(TICK) pg.image.save(scr, f'./images/scr_{t:04}.png') t += 1 pg.quit() if __name__ == '__main__': run()